Estimation of spatial distribution and symmetry of textile materials using lacunarity
DOI:
https://doi.org/10.25367/cdatp.2020.1.p180-185Keywords:
Lacunarity, Succolarity, Structural analysis, Knitted fabrics, Microscopic imagesAbstract
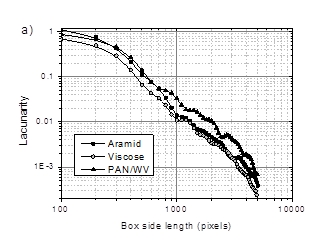
Numerical classification of textile materials, aramid, viscose, and PAN/WV, is proposed using lacunarity analysis of monochromatic digital representation of optical microscopic images. The method is sensitive to the spatial distribution of fibers, and equivalently, to the empty spaces between them. This means that lacunarity is able to quantitatively express a given level of spatial in-plane symmetries of single-face fabrics.
References
Blachowicz, T.; Ehrmann, A.; Domino, K. Statistical analysis of digital images of periodic fibrous structures using generalized Hurst exponent distributions. Physica A, 2016, 452, 167-177. DOI: 10.1016/j.physa.2016.02.013.
Mandelbrot, B. and van Ness, J. W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422-437.
Blachowicz, T.; Cwikiel, K.; Binkowski, M.; Zghidi, H. Analysis of the three-dimensional TGS crystal spatial inhomogeneity of the fractal structure, Chaos Solitons Fractals 2015, 75, 185–190. DOI: 10.1016/j.chaos.2015.02.023.
de Melo, R. H. C., Conci, A. How succolarity could be used as another fractal measure in image analysis, Telecommun. Sys. 2013, 52, 1643-1655. DOI: 10.1007/s11235-011-9657-3.
Plotnik, R. E.; Gardner, R. H.; Hargrove, W. W.; Prestegaard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis for spatial patterns. Phys. Rev. E 1996, 53, 5461-5468. DOI: 10.1103/PhysRevE.53.5461.
Reiss, M. A.; Lemmerer, B.; Hansmeier, A.; Ahammer, H. Tug-of-war lacunarity – A novel approach for estimating lacunarity. Chaos 2016, 26, 113102. DOI: 10.1063/1.4966539.
Gonzalez-Vazquez, J. P.; Anta, J. A.; Bisquert, J. Random walk numerical simulation for hopping transport at finite carrier concentrations: diffusion coefficient and transport energy concept. Phys. Chem. Chem. Phys. 2009, 11, 10359–10367. DOI: 10.1039/B912935A.
Montes-Saralegui, M.; Nikoubashman, A.; Kahl, G. Hopping and diffusion of ultrasoft particles in cluster crystals in the explicit presence of a solvent. J. Phys.: Condens. Matter 2013, 25, 195101. DOI: 10.1088/0953-8984/25/19/195101.
Yang, Ji-H.; Park, Ji-S.; Kang, J.; Wei, Su-H. First-principles multiple-barrier diffusion theory: The case study of interstitial diffusion in CdTe, Phys. Rev. 2015, B91, 075202. DOI: 10.1103/PhysRevB.91.075202.
Grassberger, P. Chaos and diffusion in deterministic cellular automata. Physica D 1984, 10, 52–58. DOI: 10.1016/0167-2789(84)90248-3.
Gaspard, P.; Klages, R. Chaotic and fractal properties of deterministic diffusion–reaction processes. Chaos 1998, 8, 409–423. DOI: 10.1063/1.166323.
Suzuki, Y., Sukigara, S. Mechanical and tactile properties of plain knitted fabrics produced from rayon vortex yarns. Text. Res. J. 2013, 83, 740-751. DOI: 10.1177/0040517512467132.
Luo, L.; Lin, H. Lacunarity and fractal analyses of soil macropores and preferential transport using micro-X-ray computed tomography. Vadose Zone Journal 2009, 8, 233–241. DOI: 10.2136/vzj2008.0010.
Kilic, K. I.; Abiyev, R. H. Exploiting the synergy between fractal dimension and lacunarity for improved texture recognition. Signal Processing 2011, 91, 2332-2344. DOI: 10.1016/j.sigpro.2011.04.018.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2020 Communications in Development and Assembling of Textile Products
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
